Now we will see how to solve one puzzle.

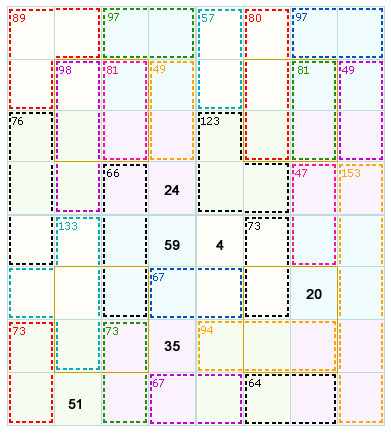
In the above puzzle square we have marked certain group of cells in the same colour and indicated their sum in one of them.

First see what the clues most visible in the above puzzle are.

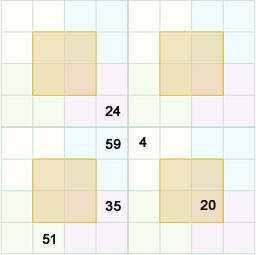
Now look for the numbers from the clues.
Always remember the rule 130 and also the template.
The template for this magic square puzzle is given below:

The above figure means that if you add the four numbers found in the cells which are colored similarly they give a magic sum of 130.

The above figure means that if you add the four numbers found in the cells which are colored in the same colour they will also give the magic sum of 130.

Now we will see how to solve the puzzle based upon the clues given in the puzzle and also from the template designs as found in the above 2 figures.

Let us take the instance of the first row. It contains two cages of 89 (3 cells) and 97 (2 cells).

By the horizontal rule the magic sum of each 4x4 should be 130. That is the sum of four cells in the horizontal or in the vertical and the diagonal cells in a 4x4 should give a sum of 130. Here four cells of the row 1 are marked and also one more cell from the row 2 is marked.

So the addition of these five cells gives the total of 186.

Any row or column or diagonal of any 4x4 sub square should give the magic sum of 130 and any row, column and diagonal of any 8x8 square should give the magic sum of 260.

By this rule the fifth number (row2, col 1) should be 56.

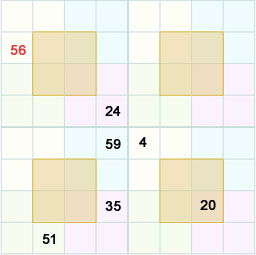
You can concentrate in one 4x4 first and then go to the other 4x4 subsquares or you can juggle between the squares.

I would prefer to juggle between the squares.

Consider this portion of the sub square 1:

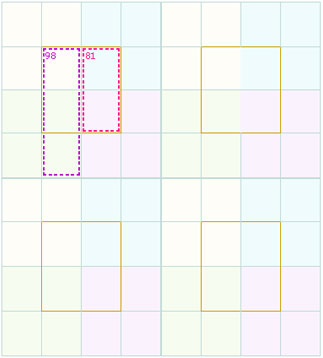
As per the template

The center 2x2 should give the magic sum of 130. here we are having five cells marked and they give a total of 179..
Therefore the cell row4, col 2 in the first subsquare should give a total of 49..

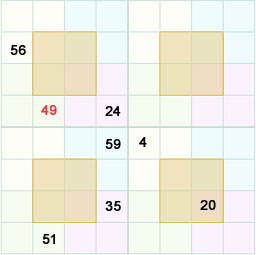
Consider the following part of the puzzle.

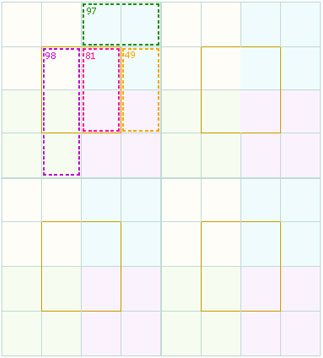
The column 4 of subsquare 1 gives a clue for the number in the row 1, columns 2 and 3.

If you observe the above square then in the column 4 the three cells give a total of 73. then the number in the row1 col 4 is 57 and row 1 col 3 is (97 – 57) = 40.

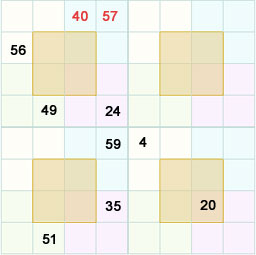
Likewise the row 4 col 3 of the sub square 1 is 9.

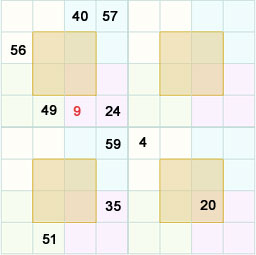
Now as per the rule d + p = e + i.

From the figure

57 + 24 = 56 + i
Therefore i = 25.

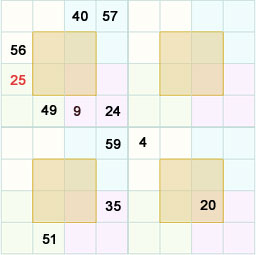
Now we can fill the row 4 as we know three numbers out of four.

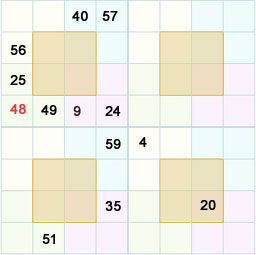
Now we can also fill up the row 1, col 1 as we know 3 out of 4 numbers of the col 1.

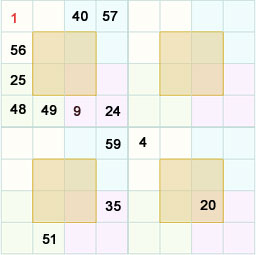
We can also fill up the row 1 col 1 and the row 1,col 2 using these two formulas.

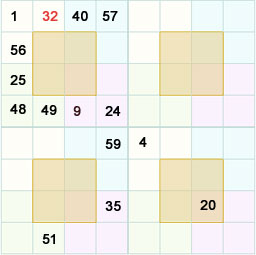
a+d = n+o
and
b+c = m+p

using these formulas also we could have obtained the square given above.
Now we can fill the col 2 either by following the rules
m+d = f + k and a + p = j + g

or by following the templates

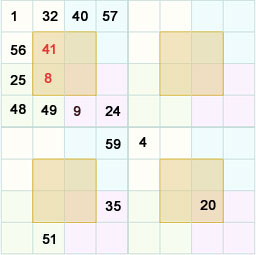
Now you can solve the above square either by following the rules

m+d = f + k and a + p = j+g from the square given below 

Or by following the rules

a + c +i + j  = 130 or e + g + m + o = 130.

We get the following square.

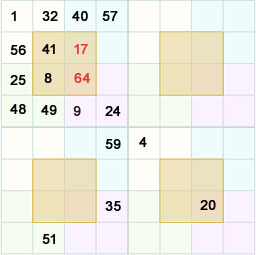
We could also employ the following template if we found out any one of the numbers given above.

Suppose we find the number 17 employing the formula

e + g + m + o = 130

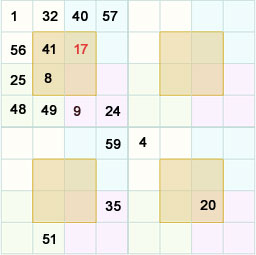
Now we can use the following template to find the 4th number.

The center 2x2 of any 4x4 magic square should give the magic sum.

Using this rule also we can find the 4th number and get the square

Now we have 3 out of 4 numbers in the row 2 and row 3. we can find the 4th number straightaway or we can use the templates to find out the 4th number

or we can use the templates to find out the 4th number

We can also use the formula

f+h+n+p = 130
and
b+d+j+l = 130.

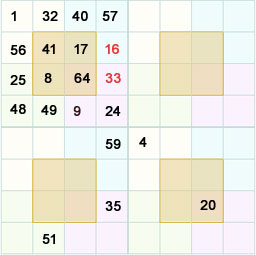
Now we have obtained the first sub square.

Likewise we can obtain all the 4 sub squares.